About

I am an Applied Mathematics PhD candidate at North Carolina State University, a DOE-funded research assistant, and an intern at Sandia National Labs. My work develops scalable, mathematically rigorous methods for PDE-governed systems, with a focus on uncertainty quantification, inference, and prediction.
Advisor: Alen Alexanderian
Email: jnneuber@ncsu.edu
CV: Download CV
Research
I work at the intersection of infinite-dimensional Bayesian inverse problems, optimal experimental design (OED), and large-scale uncertainty quantification with PDE models. The aim is to place sensors and choose experiments so that inference and prediction quality improve at minimum cost, with algorithms that scale on HPC.
Interests
- Bayesian inverse problems in infinite dimensions; low-rank methods and randomized linear algebra
- OED and decision-focused UQ in PDE-governed systems
- Path/trajectory optimization of mobile sensors for inference
- High-performance scientific computing and software for large inverse problems
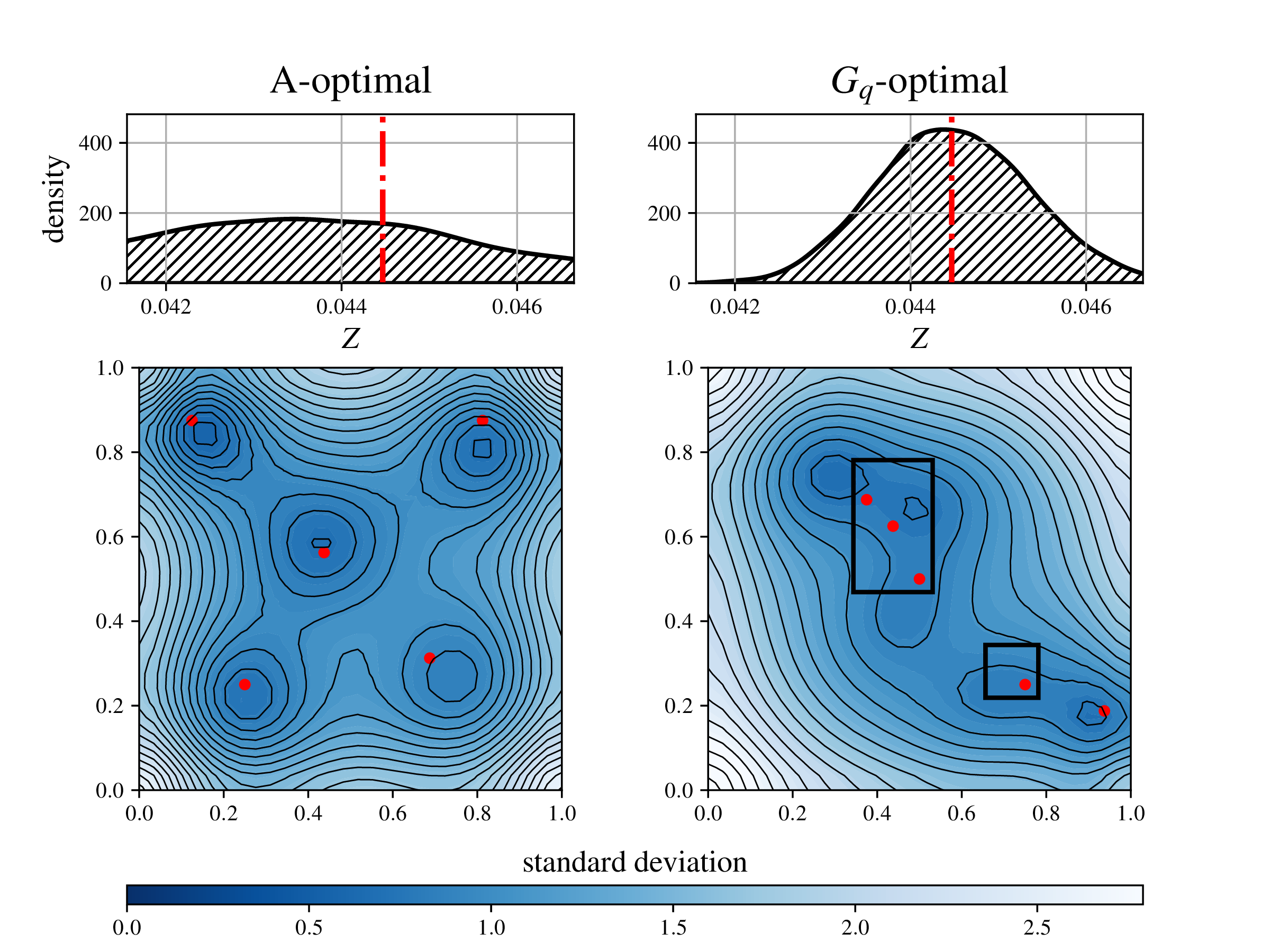
A-optimal vs. Gq-optimal designs for a Bayesian inverse problem with posterior variance fields and goal densities.
Illustrative Visualizations
My research involves developing visualizations for diagnostics and decision making. These include depictions of uncertainty across space and time, interactive and GUI-based figures, and methods for exploring complex, high-dimensional PDE-governed systems. Below is an animation of a time-reversed vortex flow benchmark for the level-set equation, along with a spatio-temporal variance field corresponding to an optimal sensor path.
Publications
- Goal-oriented optimal design of infinite-dimensional Bayesian inverse problems using quadratic approximations.
J.N. Neuberger, A. Alexanderian, B. van Bloemen Waanders. Journal of Scientific Computing (accepted); preprint available. - Optimal design of sensor trajectories for infinite-dimensional Bayesian inverse problems.
J.N. Neuberger, A. Alexanderian, B. van Bloemen Waanders, A. Attia. Manuscript in preparation. - Computational aspects of optimal experimental design for large-scale Bayesian linear inverse problems.
N. Neuberger, B. van Bloemen Waanders, A. Alexanderian. CSRI Summer Proceedings, Sandia National Laboratories, 2023. - An Elementary Proof of Weisman’s Congruence When p = 2.
N. Neuberger, B. Yildiz. PUMP Journal of Undergraduate Research, 2020.
Contact
North Carolina State University • Sandia National Laboratories (CCR)
Email: jnneuber@ncsu.edu • CV: Download CV